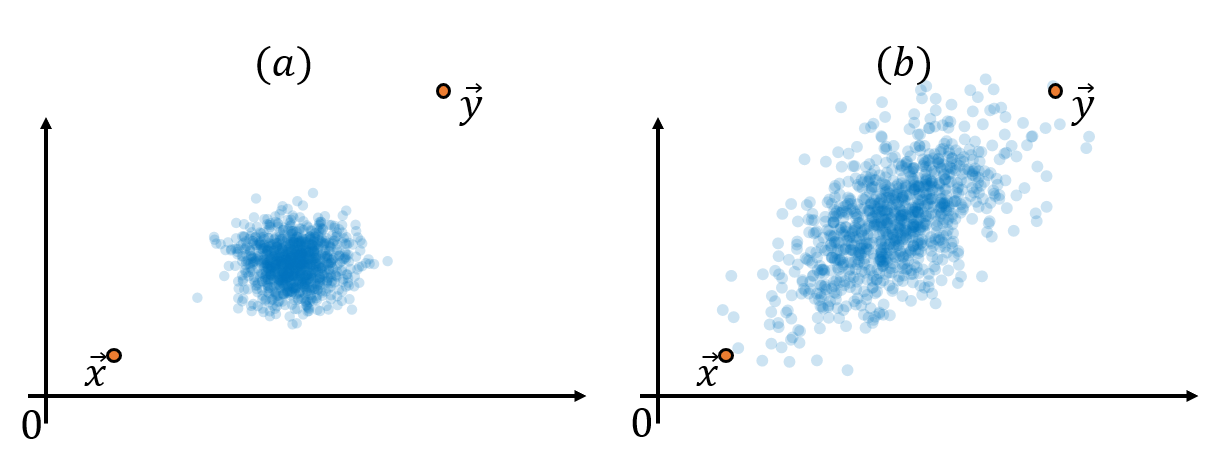[Data Analysis] 거리 기반 이상 탐지

거리기반 이상탐지를 정리했습니다.

게시 2025/02/23

By 황병현

14 분읽는 시간

거리기반 이상 탐지

공통
- 카테고리컬 데이터에 대해서는 취약하다.(One-Hot Encoding, Labeling 등) : 이는 거리에 영향을 줄 수 있음
- 거리 기반으로 영향을 받기에 변수의 값(Ex. 잎의 높이(5cm), 넓이(1.2cm))이 적절하게 조절되어야함. 정규화 고려(MinMaxScaler, StandardScaler 등)
- 모든 값의 거리를 계산하기에 데이터 양이 많으면 시간이 오래걸림. 또한 다시 재학습 시키면 처음부터 다시 학습을 시켜야함.

마할라노비스 거리 이상 탐지

마할라노비스 거리(Mahalanobis distance)는 다변량 공간에서 두 점 사이의 거리를 의미한다. 유클리디안 거리와의 차이점은 두 점 사이의 분포, 즉 두 변수간의 상관관계(공분산)를 고려해서 측정한 거리라는 것.

(a)의 그림의 경우 파란색 데이터의 분포에서 상당히 벗어나있다는 것을 알 수 있다. 반면에 (b)는 파란색 데이터의 분포에서 상대적으로 덜 벗어난 곳에 위치해있다. 즉 다른 데이터들의 분포를 고려하면 (a)에 있는 두 벡터 x와 y 간의 거리가 (b)에 있는 두 벡터 간의 거리보다 더 멀다고 볼 수 있다.

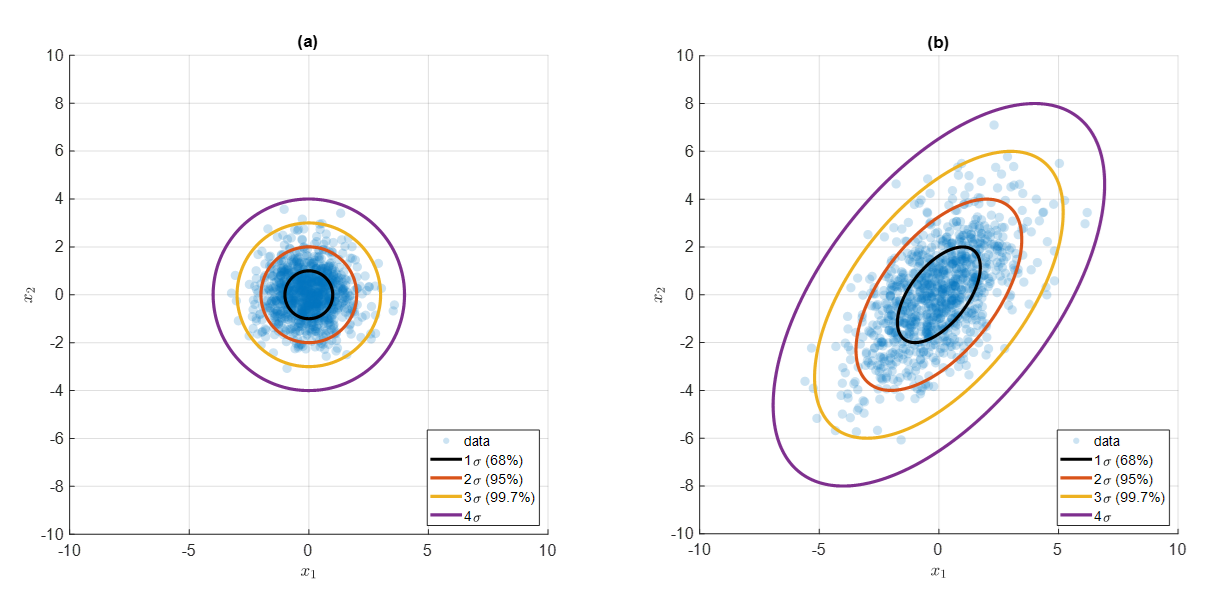
만약 데이터의 분포를 정규분포의 형태라고 가정할 수 있다면 정규분포의 표준 편차의 성질을 이용해 다음과 같이 평균(중심)으로부터 1, 2, 3 표준편차 만큼 떨어진 곳에 68, 95, 99.7%(3-sigma rule)만큼의 데이터가 들어온다는 사실을 이용할 수 있다.

평균으로부터 68, 95, 99.7% 등 표준편차 만큼 떨어진 거리를 등고선으로 표시한 그림으로 (b)에 있는 타원의 형태를 그림 4의 (a)에 있는 단위원으로 축소시킨다면 표준 편차를 정규화 시킬 수 있다.

벡터 공간의 변형은 행렬로 표현할 수 있다. 특히, 데이터의 “맥락”을 표현하는 행렬은 공분산 행렬( Σ )과 관련되어 있고, 그것을 다시 돌려 놓기 위한 행렬은 공분산 행렬의 역행렬( Σ − 1 )과 관련되어 있다.

장점
- 데이터의 분포를 고려한 이상치 탐기 가능
- 비선형 관계의 데이터에 활용 가능
- 데이터 자체의 가정을 할 필요 없음
단점
- 클러스터가 있는 데이터에서는 사용 불가

  
from sklearn.covariance import EllipticEnvelope
from sklearn.datasets import make_blobs

import pandas as pd
import numpy as np

# 데이터 생성, make_blobs : 가우시안 정규분포를 이용해 가상 데이터를 생성
X, _ = make_blobs(n_samples=100, n_features=2, centers=1, random_state=42)

# 이상치 생성
X[0,0] = 10
X[0,0] = 10

# EllipticEnvelope 설정, contamination : 데이터 집합에서 이상치가 차지하는 비율
ee = EllipticEnvelope(contamination=0.1)

# 이상치 탐지
ee.fit(X)
pred = ee.predict(X)

  
# DataFrame 생성
df = pd.DataFrame(X, columns=['col1', 'col2'])
df['outlier'] = pred
df.head(5)

	col1	col2	outlier
0	10.000000	9.796109	-1
1	-1.883530	8.157129	1
2	-2.441669	7.589538	1
3	-3.700501	9.670840	1
4	-2.732660	9.728287	1

  
import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline

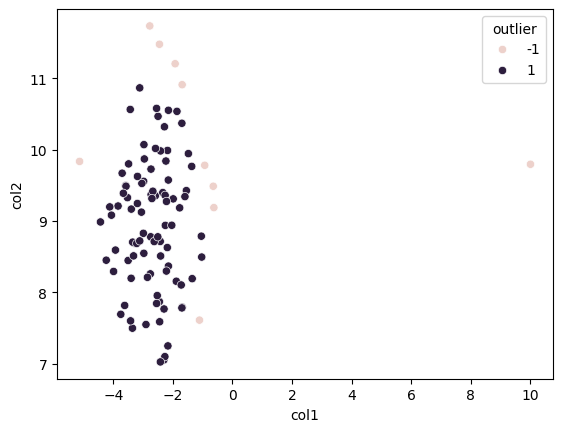
sns.scatterplot(x='col1', y='col2', hue='outlier', data=df);

K-Mean 이상 탐지

데이터를 여러 개의 클러스터로 나누고, 각 클러스터 중심에서의 거리를 기반으로 이상치를 탐지. 클러스터에 속하지 않거나 클러스터 중심에서 멀리 떨어진 데이터 포인트를 이상치로 간주.

K개의 임의의 중심점(centroid)을 배치한다.
각 데이터들을 가장 가까운 중심점으로 할당한다. (일종의 군집을 형성한다.)
군집으로 지정된 데이터들을 기반으로 해당 군집의 중심점을 업데이트한다.
2번, 3번 단계를 수렴이 될 때까지, 즉 더이상 중심점이 업데이트 되지 않을 때까지 반복한다.

장점
- 비지도학습 방법에 속한다.
- 특정 변수에 대한 역할 정의가 필요 없음
- 포인트와 그룹간의 거리계산만을 하기 떄문에 적은 계산량을 사용함(속도 빠름)
단점
- 여러번 실행해야함
- 노이즈와 아웃라이어에 매우 민감하게 반응함. 아웃라이어 떄문에 중심점이 이동할 수 있음(주의 필요)
- 랜덤하게 정해지는 초기 중심정으로 인해 매번 결과가 달라질 수 있다.

  
from sklearn.cluster import KMeans

# K-Mean 설정, n_clusters : 형성할 클러스터의 수, n_init : K-Means 알고리즘을 실행할 횟수
kmeans = KMeans(n_clusters=2, random_state=42, n_init="auto")

kmeans.fit(X)
pred = kmeans.predict(X)

  
# DataFrame 생성
df = pd.DataFrame(X, columns=['col1', 'col2'])
df['outlier'] = pred
df.head(5)

	col1	col2	outlier
0	10.000000	9.796109	1
1	-1.883530	8.157129	0
2	-2.441669	7.589538	0
3	-3.700501	9.670840	0
4	-2.732660	9.728287	0

  
import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline

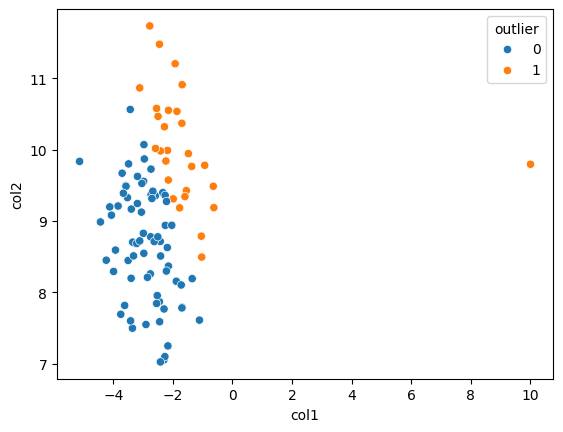
sns.scatterplot(x='col1', y='col2', hue='outlier', data=df);

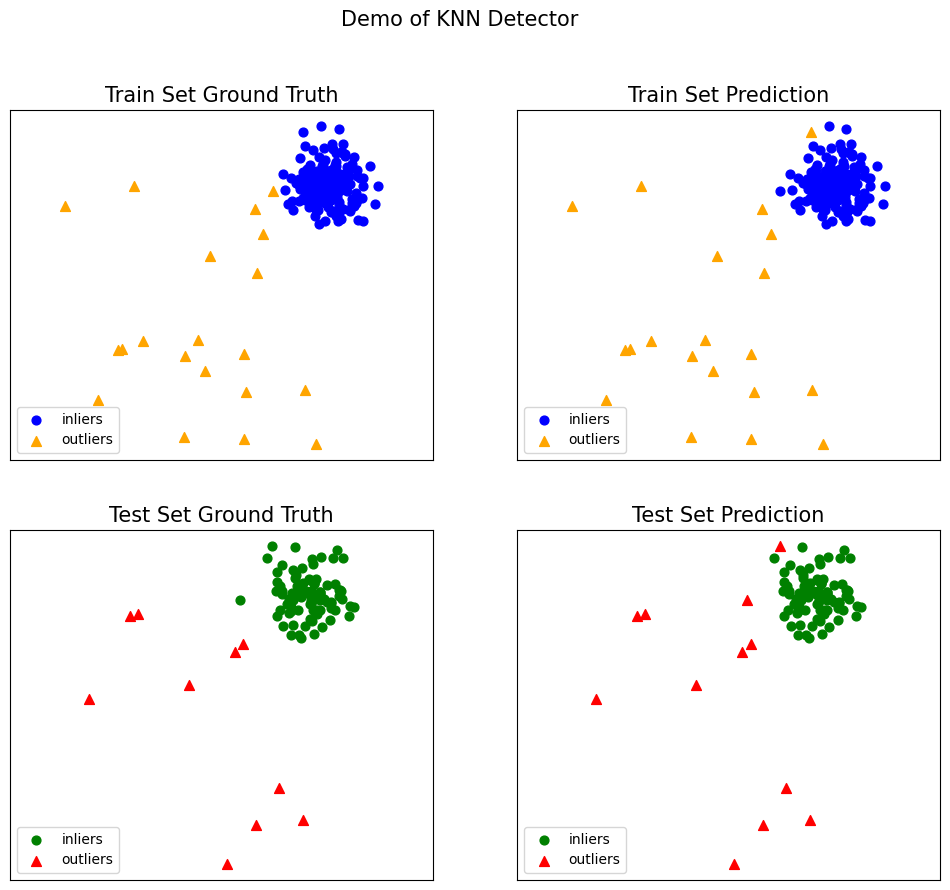
KNN 이상 탐지

알고리즘은 각 데이터 포인트에 대해 가장 가까운 K개의 이웃을 찾고, 이 이웃들 간의 거리 정보를 기반으로 해당 데이터 포인트의 특성을 판단하는 지도 학습 알고리즘

새로운 데이터 포인트에서 가장 가까운 K개를 선택한다.
K개의 이웃 중 가장 많은 label을 새로운 데이터 포인트로 예측한다.

장점
- 기존 분류 체계 값을 모두 검사하여 비교하므로 높은 정확도
- 기존 데이터를 기반으로 하기 때문에 데이터에 대한 가정이 없음
- 이해하고 구현하기 쉬움.
단점
- 특징과 클래스간 관계를 이해하는데 제한적

  
from pyod.utils.example import visualize
from pyod.utils.data import evaluate_print
from pyod.utils.data import generate_data
from pyod.models.knn import KNN

  
contamination = 0.1  # 이상치 비율
n_train = 200  # training 데이터 갯수
n_test = 100  # testing 데이터 갯수

# 데이터 생성
X_train, X_test, y_train, y_test = \
    generate_data(n_train=n_train,
                  n_test=n_test,
                  n_features=2,
                  contamination=contamination,
                  random_state=42)

X_test.shape, y_test.shape

((100, 2), (100,))

  
clf_name = 'KNN'
clf = KNN()
clf.fit(X_train)

KNN(algorithm='auto', contamination=0.1, leaf_size=30, method='largest',
  metric='minkowski', metric_params=None, n_jobs=1, n_neighbors=5, p=2,
  radius=1.0)

  
y_train_pred = clf.labels_
y_train_scores = clf.decision_scores_

y_test_pred = clf.predict(X_test)
y_test_scores = clf.decision_function(X_test)

print("On Training Data:")
evaluate_print(clf_name, y_train, y_train_scores)

print("\nOn Test Data:")
evaluate_print(clf_name, y_test, y_test_scores)

On Training Data:
KNN ROC:0.9992, precision @ rank n:0.95

On Test Data:
KNN ROC:1.0, precision @ rank n:1.0

  
visualize(clf_name, X_train, y_train, X_test, y_test, y_train_pred,
          y_test_pred, show_figure=True, save_figure=True)

K-Mean와 KNN의 차이점

K-Means: 데이터를 클러스터로 그룹화하여 각 클러스터 내의 밀집도를 기반으로 이상치를 탐지합니다. 주로 군집화를 통해 데이터의 구조를 파악하고 이상치를 탐지합니다.

사용 방식: 데이터 전체를 클러스터로 그룹화하고 클러스터 중심에서의 거리를 기반으로 이상치를 판단합니다.
- 군집화 여부: 명확한 클러스터를 형성하여 클러스터 내의 거리를 평가합니다.

KNN: 각 데이터 포인트의 이웃과의 거리를 기반으로 밀도를 평가하여 이상치를 탐지합니다. 주로 개별 데이터 포인트의 밀도를 평가하여 이상치를 탐지합니다.

사용 방식: 각 데이터 포인트의 이웃과의 거리를 계산하여 밀도를 평가하고, 밀도가 낮은 포인트를 이상치로 판단합니다.
- 군집화 여부: 클러스터를 형성하지 않고, 각 데이터 포인트의 이웃과의 거리를 직접 평가합니다.

LOF 이상 탐지

LOF(Local Outlier Factor)알고리즘은 주어진 데이터 포인트의 이웃에 대한 로컬 밀도 편차를 계산하는 비지도 이상치 감지 알고리즘

주변 데이터 포인트들의 밀도를 비교하여 상대적으로 밀도가 낮은 점들을 이상값(outlier)으로 판단

각 데이터 k개의 가장 가까운 이웃(k-nearest neighbors, k-NN) 을 찾는다.
특정 점 𝑜 o가 다른 점 𝑝 p로부터 얼마나 접근 가능한지를 측정한다.
- Reachability Distance 계산
특정 점 𝑝 p의 지역 밀도를 구한다.
- Local Reachability Density (LRD) 계산
특정 점 𝑝 p의 LOF 값은 주변 이웃들의 지역 밀도 대비 𝑝 p의 지역 밀도 비율로 정의
- LOF 계산

LOF 값이 1에 가까우면 정상 데이터
1보다 크면 이상치 가능성 높음
LOF 값이 매우 크면 이상치(Outlier)로 판단
장점
- 밀접한 클러스터에서 조금만 떨어져 있어도 이상치로 탐지
- 비지도학습에서 사용 가능
단점
- 차원 수가 증가할 수록 계산량 증가
- 이상치 판단 기준 설정 어려움 (여러 클러스터가 존재한다면 민감하게 반응)

  
import numpy as np
import matplotlib.pyplot as plt
from sklearn.neighbors import LocalOutlierFactor
from matplotlib.pyplot import figure

  
np.random.seed(42)

# 데이터 생성
X_inliers = 0.3 * np.random.randn(100, 2)
X_inliers = np.r_[X_inliers + 2, 2*X_inliers - 2] #각각 2,2 혹은 -2,-2만큼 평행이동한거를 vstack. 즉 cluster 2개

X_outliers = np.random.uniform(low=-4, high=4, size=(20, 2))
X = np.r_[X_inliers, X_outliers]#-4,4에서 뽑은 outlier와 inlier를 vstack

n_outliers = len(X_outliers)
ground_truth = np.ones(len(X), dtype=int)
ground_truth[-n_outliers:] = -1

  
clf = LocalOutlierFactor(n_neighbors=20, contamination=0.1)
y_pred = clf.fit_predict(X)
n_errors = (y_pred != ground_truth).sum()
X_scores = clf.negative_outlier_factor_

  
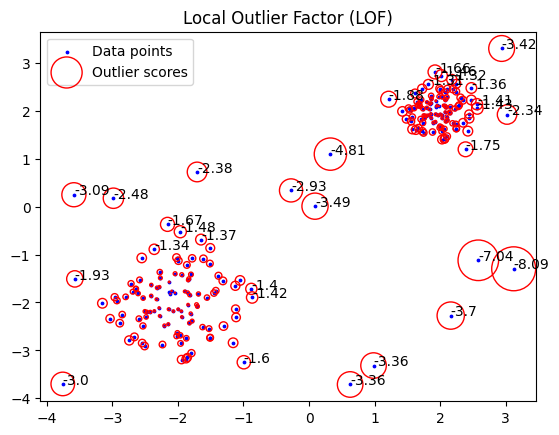
plt.title("Local Outlier Factor (LOF)")
plt.scatter(X[:, 0], X[:, 1], color='b', s=3., label='Data points')

radius = (X_scores.max() - X_scores) / (X_scores.max() - X_scores.min()) #minmax scaling
plt.scatter(X[:, 0], X[:, 1], s=1000 * radius, edgecolors='r',
            facecolors='none', label='Outlier scores')
n=np.copy(X_scores)
n[n>-1.3]=np.nan
n=np.round(n,2)
for i, txt in enumerate(n):
    if np.isnan(txt):continue
    plt.annotate(txt, (X[i,0], X[i,1]))
legend = plt.legend(loc='upper left')
plt.show()

참고자료

Data Analysis, Anomaly Detection