[Data Analysis] 통계적 기법 이상 탐지

통계적 기법으로 이상탐지

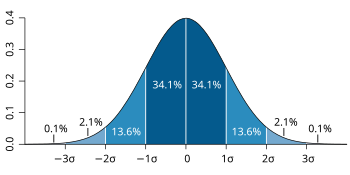
3-Sigma Rule (68–95–99.7 rule)

• 정규 분포에서 데이터의 99.7%가 평균으로부터 3시그마 이내에 위치함을 설명하는 규칙

• 장점
  • 구현하기 쉽다.
  • 명확한 기준을 설정할 수 있기 때문에, 방법론에 재학습 필요없음
• 단점
  • 정규분포가 가정되어야 함
  • 타차원 데이터에 적용하기 어려움
  • 단변량 데이터에 적용할 수 있으며, Feature간 상관관계 파악하기 어려움

from sklearn.datasets import load_iris
import pandas as pd
import numpy as np

iris = load_iris()
datasets = pd.DataFrame(iris.data, columns=iris.feature_names)
datasets['target'] = iris.target

datasets

	sepal length (cm)	sepal width (cm)	petal length (cm)	petal width (cm)	target
0	5.1	3.5	1.4	0.2	0
1	4.9	3.0	1.4	0.2	0
2	4.7	3.2	1.3	0.2	0
3	4.6	3.1	1.5	0.2	0
4	5.0	3.6	1.4	0.2	0
...	...	...	...	...	...
145	6.7	3.0	5.2	2.3	2
146	6.3	2.5	5.0	1.9	2
147	6.5	3.0	5.2	2.0	2
148	6.2	3.4	5.4	2.3	2
149	5.9	3.0	5.1	1.8	2

150 rows × 5 columns

# 데이터 분포 확인
datasets.describe()

	sepal length (cm)	sepal width (cm)	petal length (cm)	petal width (cm)	target
count	150.000000	150.000000	150.000000	150.000000	150.000000
mean	5.843333	3.057333	3.758000	1.199333	1.000000
std	0.828066	0.435866	1.765298	0.762238	0.819232
min	4.300000	2.000000	1.000000	0.100000	0.000000
25%	5.100000	2.800000	1.600000	0.300000	0.000000
50%	5.800000	3.000000	4.350000	1.300000	1.000000
75%	6.400000	3.300000	5.100000	1.800000	2.000000
max	7.900000	4.400000	6.900000	2.500000	2.000000

# UCL(Upper Control Limit), LCL(Lower Control Limit) 생성
datasets["UCLpental_length"] = datasets["petal length (cm)"].mean() + 2 * datasets["petal length (cm)"].std()
datasets["LCLpental_length"] = datasets["petal length (cm)"].mean() - 2 * datasets["petal length (cm)"].std()

datasets["LCL_pental_width"] = datasets["petal width (cm)"].mean() - 2 * datasets["petal width (cm)"].std()
datasets["UCL_pental_width"] = datasets["petal width (cm)"].mean() + 2 * datasets["petal width (cm)"].std()

datasets

	sepal length (cm)	sepal width (cm)	petal length (cm)	petal width (cm)	target	UCLpental_length	LCL_pental_width	LCLpental_length	UCL_pental_width
0	5.1	3.5	1.4	0.2	0	7.288596	-0.325142	0.227404	2.723809
1	4.9	3.0	1.4	0.2	0	7.288596	-0.325142	0.227404	2.723809
2	4.7	3.2	1.3	0.2	0	7.288596	-0.325142	0.227404	2.723809
3	4.6	3.1	1.5	0.2	0	7.288596	-0.325142	0.227404	2.723809
4	5.0	3.6	1.4	0.2	0	7.288596	-0.325142	0.227404	2.723809
...	...	...	...	...	...	...	...	...	...
145	6.7	3.0	5.2	2.3	2	7.288596	-0.325142	0.227404	2.723809
146	6.3	2.5	5.0	1.9	2	7.288596	-0.325142	0.227404	2.723809
147	6.5	3.0	5.2	2.0	2	7.288596	-0.325142	0.227404	2.723809
148	6.2	3.4	5.4	2.3	2	7.288596	-0.325142	0.227404	2.723809
149	5.9	3.0	5.1	1.8	2	7.288596	-0.325142	0.227404	2.723809

150 rows × 9 columns

import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline

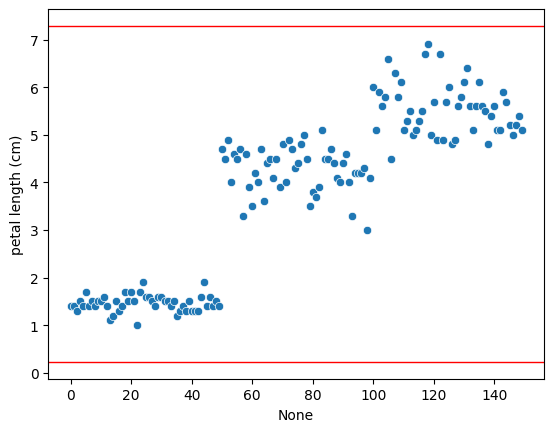
# petal length (cm) plot
sns.scatterplot(x= datasets.index, y = datasets["petal length (cm)"])
plt.axhline(y=datasets["UCLpental_length"][0], color="r",  linewidth=1)
plt.axhline(y=datasets["LCLpental_length"][0], color="r",  linewidth=1)
plt.show()

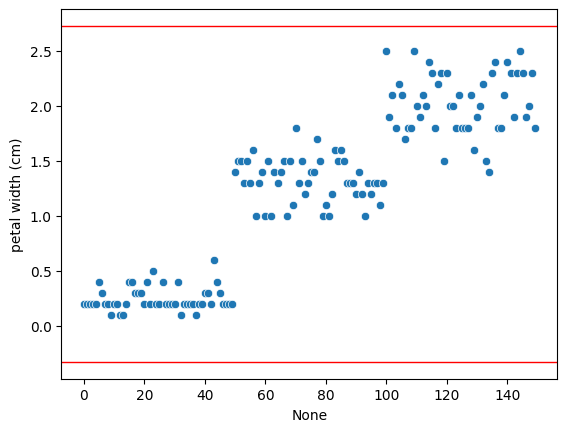
# petal width (cm) plot
sns.scatterplot(x= datasets.index, y = datasets["petal width (cm)"])
plt.axhline(y=datasets["UCL_pental_width"][0], color="r",  linewidth=1)
plt.axhline(y=datasets["LCL_pental_width"][0], color="r",  linewidth=1)
plt.show()

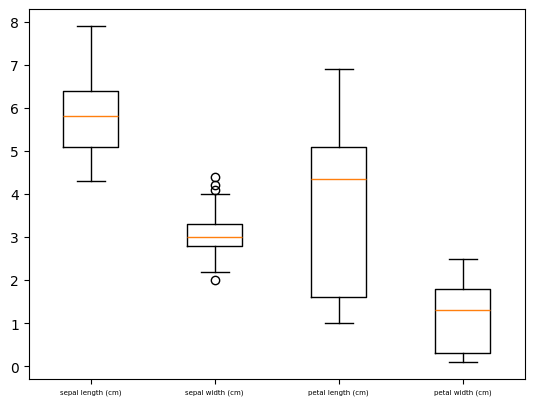
Box plot

• Box plot은 최소 정상값(min), 1사분위수(Q1), 중앙값, 3사분위수(Q3), 최대 정상값(max)를 나타내는 시각화 방법

• 장점
  • 그림을 이용해 데이터의 범위를 빠르게 파악
• 단점
  • 위치정보를 기반으로 보이기 때문에 분포를 확인하기 어려움

용어

• median - 중앙값
• IQR : 25% ~ 75%에 해당한 부분
• 75th Percentile : 제 3사분위수
• 25th Percentile : 제 1사분위수
• Whisker : 최댓값, 최솟값
• Outlier : 이상치 (Q3+1.5 IQR, Q1-1.5 IQR)

plt.boxplot([datasets["sepal length (cm)"], datasets["sepal width (cm)"],\
           datasets["petal length (cm)"], datasets["petal width (cm)"]])
plt.xticks(np.arange(1,5), iris.feature_names, fontsize = 5)
plt.show()

 

참고자료

• https://meetup.nhncloud.com/posts/366
• https://www.investopedia.com/terms/e/empirical-rule.asp