[Data Analysis] 시계열 이상 탐지(ARIMA, STL)

시계열을 통한 이상탐지 해보기

게시 2025/03/07

By 황병현

11 분읽는 시간

ARIMA 이상 탐지

ARIMA(Autoregressive Integrated Moving Average)는 시계열 데이터를 분석하고 예측하는 모델로, 자기회귀(AR), 차분(I), 이동평균(MA) 요소를 포함함.

AR(자기회귀 Autoregressive) (p) : 과거 값(시차 값)의 선형 결합. 과거 관측값을 사용하여 현재 값을 예측
I(차분 Integrated) (d) : 데이터의 정상성을 확보하기 위한 차분 연산. 비정상성을 제거하여 정상성을 확보하는 과정
MA(이동평균 Moving Average) (q) : 과거 오차 항의 선형 결합. 과거 예측 오차(잔차)를 이용하여 현재 값을 모델링

AR, I, MA 비교 요약

개념	설명	수식	역할
AR(p)	과거 값의 선형 결합을 이용	\(Y_t = c + \sum \phi_i Y_{t-i} + \epsilon_t\)	데이터의 자기상관 설명
I(d)	차분을 통해 정상성 확보	\(Y'_t = Y_t - Y_{t-1}\)	비정상성을 제거하여 분석 가능하게 만듦
MA(q)	과거 예측 오차(잔차)를 이용	\(Y_t = c + \sum \theta_i \epsilon_{t-i} + \epsilon_t\)	데이터의 단기 변동 설명

장단점

장점
- 시계열 예측에 효과적이고 해석이 용이함.
- 정상성을 확보하면 비교적 안정적인 성능을 보임.
- 계절성 변형을 추가한 SARIMA 모델도 사용 가능.
단점
- 정상성을 요구하므로 차분이 필요할 수 있음.
- 단기 예측에는 강하지만, 장기 예측에는 성능이 떨어질 수 있음.
- 이상 탐지 전용 모델이 아니므로, 추가적인 분석 필요.

ARIMA 실습

  
import pandas as pd
import numpy as np
pd.set_option('display.max_rows', 15)

from statsmodels.tsa.arima.model import ARIMA
from statsmodels.tsa.stattools import adfuller

import matplotlib.pyplot as plt
import seaborn as sns
sns.set(style="whitegrid")

  
def parser(s):
    return datetime.strptime(s, '%Y-%m-%d')

  
data = pd.read_csv('catfish.csv', parse_dates=[0], index_col=0, date_parser=parser)
start_date = datetime(1996,1,1)
end_date = datetime(2000,1,1)
data = data[start_date:end_date]
data

	Total
Date
1996-01-01	20322
1996-02-01	20613
1996-03-01	22704
1996-04-01	20276
1996-05-01	20669
...	...
1999-09-01	24430
1999-10-01	25229
1999-11-01	22344
1999-12-01	22372
2000-01-01	25412

49 rows × 1 columns

  
# 이상치 생성
data.loc["1998-12-1"]['Total'] = 10000

  
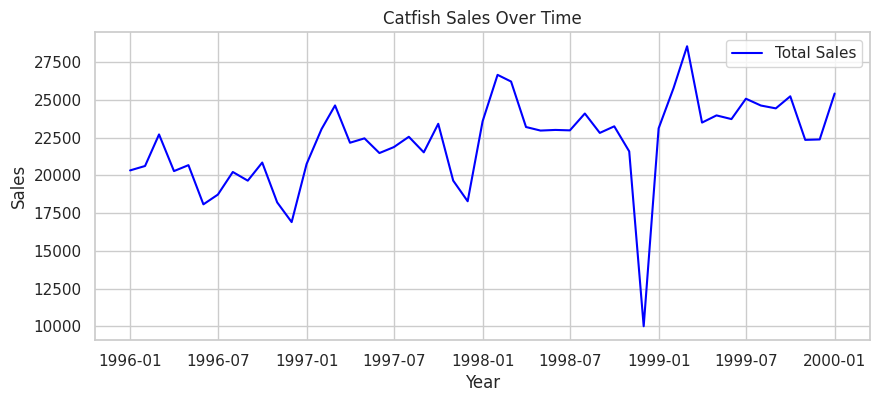
# 시계열 데이터 확인
plt.figure(figsize=(10, 4))
plt.plot(data['Total'], label="Total Sales", color='blue')
plt.xlabel("Year")
plt.ylabel("Sales")
plt.title("Catfish Sales Over Time")
plt.legend()
plt.show()

  
# 정상성 검정 (ADF 테스트) (※ p-value가 0.05 이상이면 정상성을 따름, 비정상일 시 차분 필요)
adf_result = adfuller(data['Total'])
print(f"ADF Statistic: {adf_result[0]}")
print(f"p-value: {adf_result[1]}")

ADF Statistic: -4.365679297730419
p-value: 0.0003412152022627177

# 차분 (비정상성일 경우)
# diff_series = df['Total'].diff().dropna()

  
# ARIMA 모델 적용 (p=2, d=1, q=2 설정)
model = ARIMA(data['Total'], order=(2,1,2))
model_fit = model.fit()
print(model_fit.summary())

                               SARIMAX Results                                
==============================================================================
Dep. Variable:                  Total   No. Observations:                   49
Model:                 ARIMA(2, 1, 2)   Log Likelihood                -450.993
Date:                Fri, 07 Mar 2025   AIC                            911.986
Time:                        12:31:33   BIC                            921.342
Sample:                    01-01-1996   HQIC                           915.521
                         - 01-01-2000                                         
Covariance Type:                  opg                                         
==============================================================================
                 coef    std err          z      P>|z|      [0.025      0.975]
------------------------------------------------------------------------------
ar.L1          1.4686      0.078     18.836      0.000       1.316       1.621
ar.L2         -0.5949      0.098     -6.066      0.000      -0.787      -0.403
ma.L1         -1.9447      0.116    -16.731      0.000      -2.173      -1.717
ma.L2          0.9987      0.125      8.010      0.000       0.754       1.243
sigma2      8.153e+06   2.92e-08   2.79e+14      0.000    8.15e+06    8.15e+06
===================================================================================
Ljung-Box (L1) (Q):                   0.17   Jarque-Bera (JB):               128.28
Prob(Q):                              0.68   Prob(JB):                         0.00
Heteroskedasticity (H):               2.69   Skew:                            -1.69
Prob(H) (two-sided):                  0.06   Kurtosis:                        10.26
===================================================================================

Warnings:
[1] Covariance matrix calculated using the outer product of gradients (complex-step).
[2] Covariance matrix is singular or near-singular, with condition number 7.65e+30. Standard errors may be unstable.

  
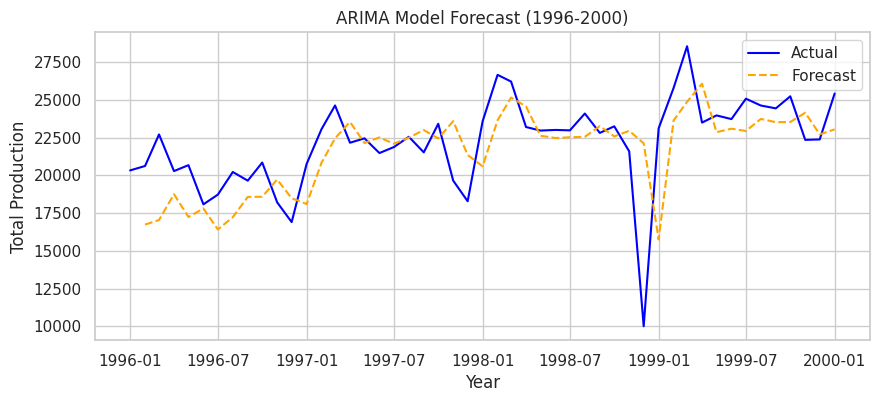
# 예측 수행
data['Forecast'] = model_fit.predict(start=1, end=len(data), dynamic=False)

# 예측 결과 시각화
plt.figure(figsize=(10, 4))
plt.plot(data['Total'], label="Actual", color="blue")
plt.plot(data['Forecast'], label="Forecast", color="orange", linestyle="dashed")
plt.xlabel("Year")
plt.ylabel("Total Sales")
plt.title("ARIMA Model Forecast (1996-2000)")
plt.legend()
plt.show()

  
from statsmodels.robust.scale import mad

# 이상값 탐지 함수 (중위수 절대 편차, MAD 사용)
def detect_anomalies(series, threshold=1.5):
    median = np.median(series)
    mad_value = mad(series)
    modified_z_score = 0.6745 * (series - median) / mad_value
    return np.abs(modified_z_score) > threshold, modified_z_score

# 이상값 탐지 수행
data['Anomaly'], check = detect_anomalies(data['Total'])

# 이상값 출력
anomalies = data[data['Anomaly']]
print("Detected Anomalies:")
print(anomalies)

Detected Anomalies:
            Total      Forecast  Anomaly
Date                                    
1996-12-01  16898  18475.216984     True
1998-12-01  10000  22116.763947     True
1999-03-01  28544  24863.487838     True

  
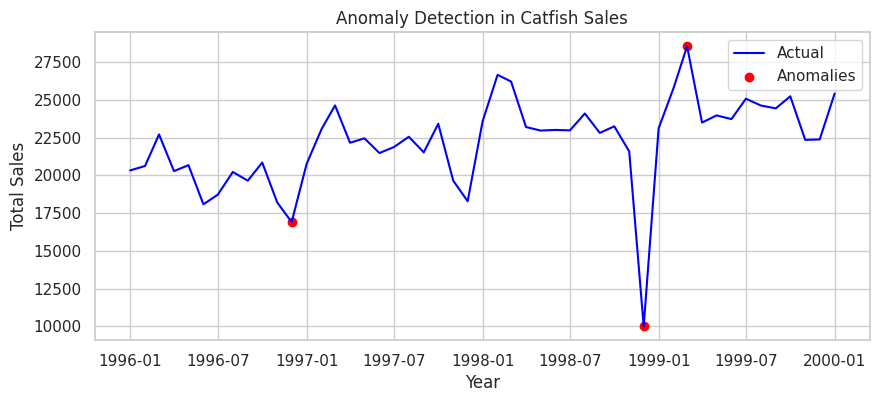
# 이상값 시각화
plt.figure(figsize=(10, 4))
plt.plot(data['Total'], label="Actual", color="blue")
plt.scatter(anomalies.index, anomalies['Total'], color="red", label="Anomalies", marker="o")
plt.xlabel("Year")
plt.ylabel("Total Sales")
plt.title("Anomaly Detection in Catfish Sales")
plt.legend()
plt.show()

STL(Seasonal Trend Decomposition using LOESS) 이상 탐지

추세(Trend) : 데이터의 장기적 움직임, series가 지남에 따라 증가, 감소 또는 비교적 안정적으로 유지되고 있는지의 여부
계졀성(Seasonality) : 고정된 간격(예: 매일, 매월 또는 매년)으로 발생하는 반복적인 패턴
주기성(Cycle) : 고정된 빈도가 아닌 형태로 증가나 감소하는 모습. 보통 이러한 요동은 경제 상황 때문에 일어나고, 흔히 “경기 순환(business cycle)”과 관련 있음
잔차(Residuals) : 다른 구성 요소에 기인할 수 없는 데이터의 무작위적 변동 또는 불규칙성. 여기에는 측정 오류, 이상치 및 기타 예상치 못한 변화가 포함.
STL에서 LOESS는 “Locally Estimated Scatterplot Smoothing”의 약자로, 데이터 포인트의 작은 창(이웃)에 회귀를 맞추어 데이터의 로컬 추세를 식별합니다. 글로벌 추세보다는 로컬 패턴에 초점을 맞추므로 이상치 및 노이즈가 있는 데이터에 대해 더욱 강력하여 진정한 이상치를 보다 정확하게 감지하는 데 도움이 됨.

STL은 Trend와 Seasonality를 제거하고 남은 Residuals을 활용하여 시계열 데이터 이상 탐지

덧셈 분해 (additive decomposition)
y = S + T + R

Trend가 일정함에 따라 변동폭이 동일하면 덧셈 분해(additive decomposition)
(※ Trend와 Seasonal의 관계가 없다.)

곱셈 분해 (multiplicative decomposition)
y = S x T x R

Trend가 상승함에 따라 변동폭이 변화하면 곱셈 분해(multiplicative decomposition)
(※ Trend변화에 따라 Seasonal의 관계가 있다.)

(※STL은 additive만 사용가능함으로 Trend와 Seasonal에 상관관계가 있으면 사용에 주의해야함)

장단점

장점
- 데이터양이 많아도 빠르게 계산이 가능
- 돌발스런 이상치에 대해 추세, 주기에 영향을 미치지 않음
단점
- 시간을 int로 변환해야 사용가능(데이터에 주말이 없으면 일자를 당겨서 사용해야함)
- Trend와 Seasonal에 상관관계가 있을 시 사용 주의
- 단변량만 사용 가능

※ STL Decomposition 관련 논문 : http://www.wessa.net/download/stl.pdf

STL 실습

  
import pandas as pd
pd.set_option('display.max_rows', 15)

import matplotlib.pyplot as plt
from datetime import datetime
import matplotlib.dates as mdates
import seaborn as sns
sns.set(style="whitegrid")

import warnings
warnings.filterwarnings('ignore')

  
data = pd.read_csv('catfish.csv', parse_dates=[0], index_col=0, date_parser=parser)

start_date = datetime(1996,1,1)
end_date = datetime(2000,1,1)
data = data[start_date:end_date]
data

	Total
Date
1996-01-01	20322
1996-02-01	20613
1996-03-01	22704
1996-04-01	20276
1996-05-01	20669
...	...
1999-09-01	24430
1999-10-01	25229
1999-11-01	22344
1999-12-01	22372
2000-01-01	25412

49 rows × 1 columns

  
# 이상치 생성
data.loc["1998-12-1"]['Total'] = 10000

  
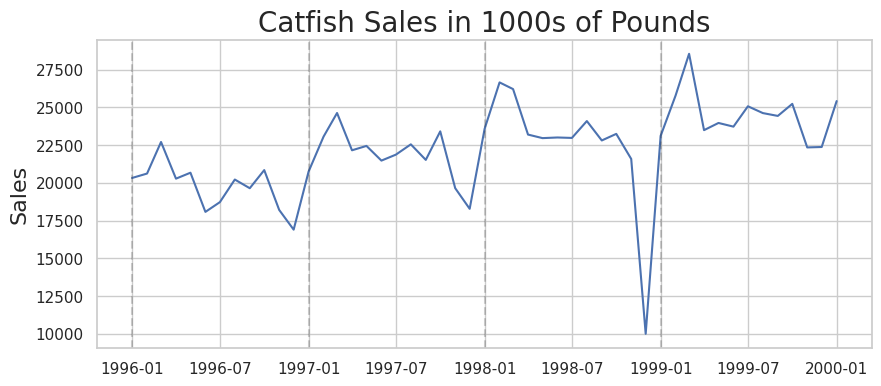
plt.figure(figsize=(10,4))
plt.plot(data)
plt.title('Catfish Sales in 1000s of Pounds', fontsize=20)
plt.ylabel('Sales', fontsize=16)
for year in range(start_date.year,end_date.year):
    plt.axvline(pd.to_datetime(str(year)+'-01-01'), color='k', linestyle='--', alpha=0.2)

  
from statsmodels.tsa.seasonal import seasonal_decompose
import matplotlib.dates as mdates

  
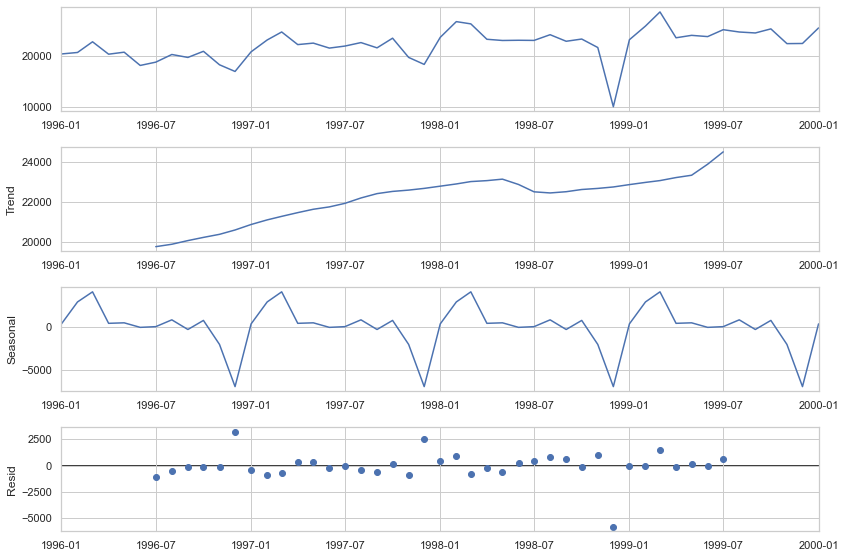
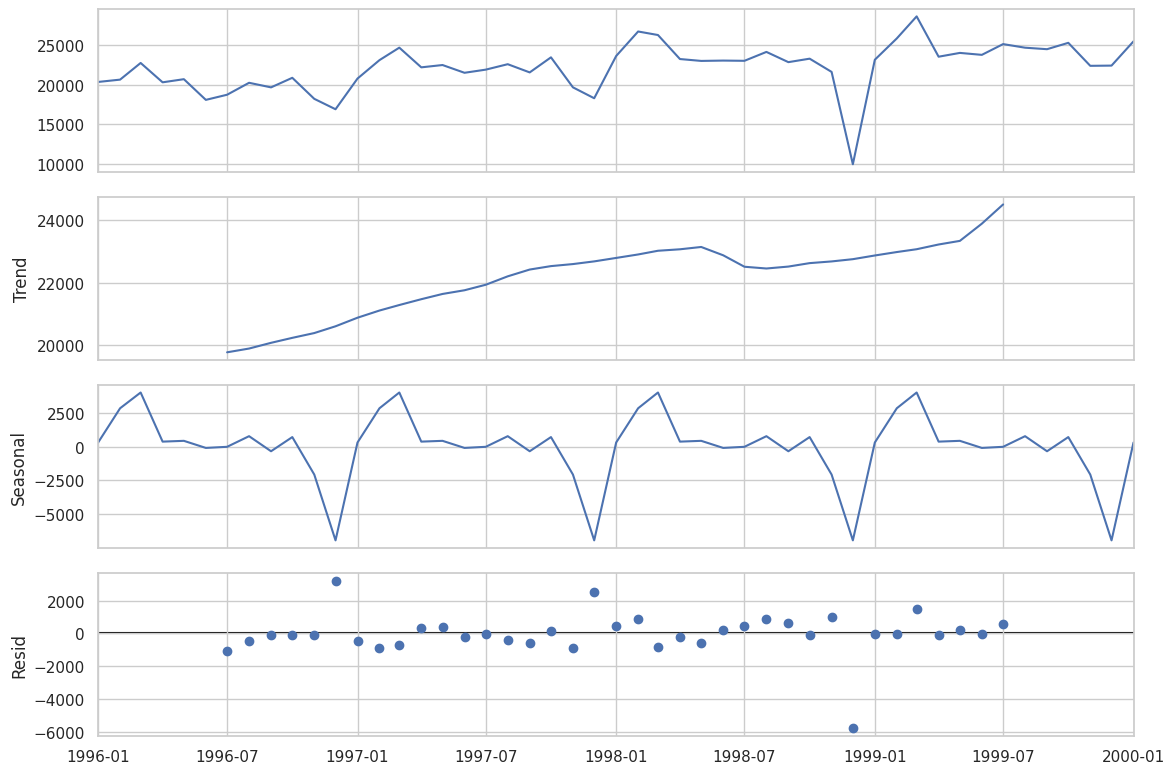
plt.rc('figure',figsize=(12,8))
plt.rc('font',size=15)

result = seasonal_decompose(data,model='additive')
fig = result.plot()

  
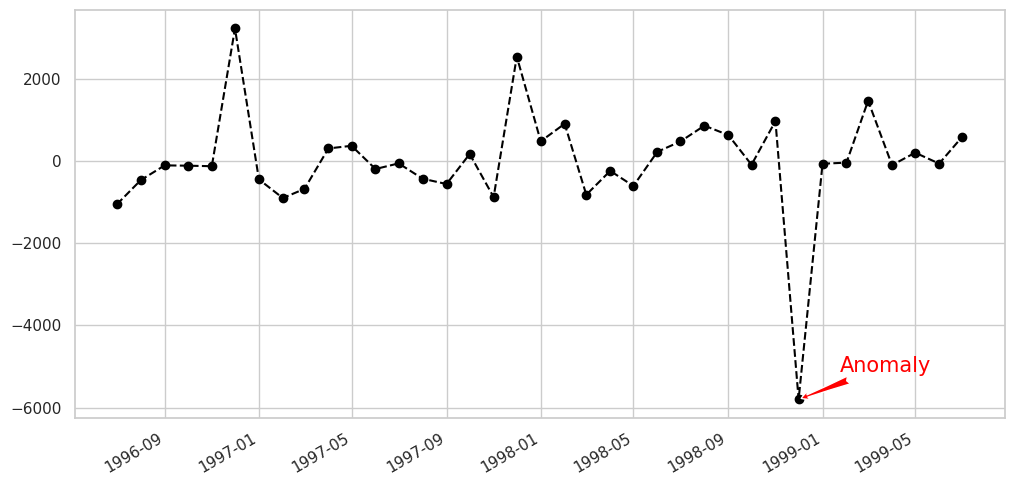
# 이상치 확인
plt.rc('figure',figsize=(12,6))
plt.rc('font',size=15)

fig, ax = plt.subplots()
x = result.resid.index
y = result.resid.values
ax.plot_date(x, y, color='black',linestyle='--')

ax.annotate('Anomaly', (mdates.date2num(x[35]), y[35]), xytext=(30, 20),
           textcoords='offset points', color='red',arrowprops=dict(facecolor='red',arrowstyle='fancy'))

fig.autofmt_xdate()
plt.show()

  
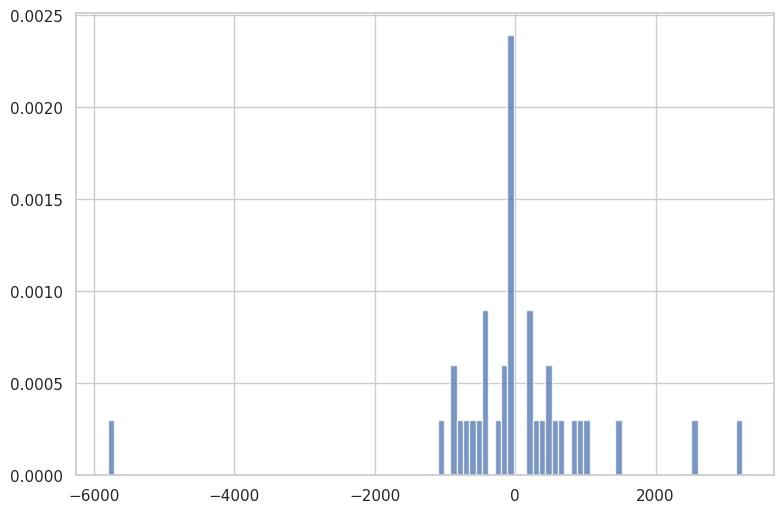
# Residual(잔차)의 분포 확인
fig, ax = plt.subplots(figsize=(9,6))
_ = plt.hist(result.resid, 100, density=True, alpha=0.75)

  
from statsmodels.tsa.seasonal import STL
# Odd num : seasonal = 13(연도별) / seasonal = 5(분기별) / seasonal = 7(주별)
stl = STL(data, seasonal=13)
res = stl.fit()

  
# 정규성 검사 (※ p-value가 0.05 이상이면 정규성을 따름)
from statsmodels.stats.weightstats import ztest
r = res.resid.values
st, p = ztest(r)
print(st,p)

-0.2533967415054412 0.799961645414213

  
mu, std = res.resid.mean(), res.resid.std()
print("평균:", mu, "표준편차:", std)

# 3-sigma(표준편차)를 기준으로 이상치 판단
print("이상치 갯수:", len(res.resid[(res.resid>mu+3*std)|(res.resid<mu-3*std)]))

평균: -41.35445919761511 표준편차: 1142.4030658937645
이상치 갯수: 1

참고자료

Data Analysis, Anomaly Detection